Employing Genetic Algorithms with Ant Colony Optimization to Solve the Travelling Salesman Problem

The Travelling Salesman Problem (TSP) is a classic optimization problem where the goal is to find the shortest possible route that visits a set of cities exactly once and returns to the origin city. It has numerous real-world applications, from logistics to robotics. In this blog, I’ll walk you through my project where I combined Genetic Algorithms (GA) and Ant Colony Optimization (ACO) to solve the TSP. I’ll explain the key components of the solution, the challenges I faced, and how I addressed them.

The Genetic Algorithm Approach

The first part of my solution uses a Genetic Algorithm to evolve a population of potential solutions (chromosomes) over multiple generations. Here’s how it works:

Key Components of the Genetic Algorithm

Initialization:

• The population is initialized with random permutations of cities, representing potential routes.
• Each chromosome is a list of city indices, shuffled randomly.

Fitness Function:

• The fitness of a chromosome is calculated as the inverse of the total distance of the route it represents. This ensures that shorter routes have higher fitness.

Selection:

• Parents are selected using a roulette wheel selection method, where chromosomes with higher fitness have a greater chance of being selected.
• This introduces randomness while favoring better solutions, helping to avoid premature convergence to local optima.

Crossover:

• Ordered crossover is used to combine two parent chromosomes into two offspring. This ensures that the offspring are valid permutations (no duplicate cities).
• The crossover points are selected randomly, and the genes between these points are swapped between the parents.

Mutation:

• Mutation is applied to introduce diversity in the population. A small probability is used to swap two randomly selected genes in a chromosome.

Reproduction:

• The new population is created by applying crossover and mutation to the selected parents. This process is repeated for a fixed number of generations.

Elitism:

• I opted not to use elitism (directly carrying over the best solutions to the next generation) to encourage exploration of the solution space. Instead, I relied on the roulette wheel selection to balance exploration and exploitation.

The Ant Colony Optimization Approach

The second part of my solution uses Ant Colony Optimization to refine the solutions found by the Genetic Algorithm. ACO is inspired by the behavior of ants searching for food, where ants deposit pheromones on paths they traverse. Over time, shorter paths accumulate more pheromones, guiding future ants to follow them.

Key Modifications to Improve ACO

Backtracking with a Stack:

• Ants maintain a stack of their previous moves. If they reach a dead end, they backtrack efficiently without revisiting nodes unnecessarily.
• This reduces redundant exploration and ensures that pheromones are deposited only on productive paths.

Heuristic-Based Movement:

• Ants prioritize paths with a lower Euclidean distance to the target, combined with pheromone levels.
• This reduces randomness and leads to more direct routes.

Limited Travel Distance:

• A maximum travel distance is imposed to prevent ants from getting stuck in locally optimal but globally suboptimal paths.
• This ensures that ants explore a broader area before converging.

Visited Dictionary:

• A dictionary tracks nodes that have been visited multiple times. Nodes visited frequently are penalized, reducing the likelihood of revisiting them.
• This minimizes loops and redundant exploration.

Momentum:

• Ants receive a boost if they move in the same direction for three consecutive steps. This encourages straight-line movement and reduces unnecessary turns.

U-Turn Penalty:

• Ants are penalized for making U-turns, which are inefficient and counterproductive.
• This ensures more purposeful movement and avoids wasteful exploration.

Combining GA and ACO

The Genetic Algorithm is used to generate an initial set of good solutions, which are then refined using Ant Colony Optimization. Here’s how the two methods complement each other:

GA for Exploration:

• The Genetic Algorithm explores a wide range of potential solutions, ensuring diversity in the population.
• It provides a good starting point for ACO by identifying promising regions of the solution space.

ACO for Exploitation:

• Ant Colony Optimization refines the solutions found by GA by exploiting the pheromone trails.
• It focuses on optimizing the routes further, ensuring that the final solution is as short as possible.

Challenges and Solutions

Challenges in Genetic Algorithms

Premature Convergence:

• Without elitism, the population can converge too quickly to suboptimal solutions.
• I addressed this by using roulette wheel selection, which introduces randomness and maintains diversity.

Slow Convergence:

• The lack of elitism can slow down convergence, as non-optimal solutions may be selected.
• I balanced this by tuning the crossover and mutation rates to ensure a good mix of exploration and exploitation.

Challenges in Ant Colony Optimization

Loops and Redundant Exploration:

• Ants can get stuck in loops or revisit the same nodes repeatedly.
• I implemented backtracking with a stack and a visited dictionary to reduce redundant exploration.

Dead Ends:

• Ants can waste time exploring paths that lead to dead ends.
• I introduced a maximum travel distance and heuristic-based movement to guide ants toward more promising paths.

Large Spaces:

• In large, open spaces, ants can wander aimlessly.
• I incorporated wall-following behavior and momentum to ensure more efficient exploration.

Results

The combination of Genetic Algorithms and Ant Colony Optimization proved to be highly effective in solving the TSP. The GA provided a diverse set of initial solutions, while the ACO refined these solutions to find the shortest possible route. The modifications I made to the ACO algorithm, such as backtracking, momentum, and U-turn penalties, significantly improved its performance.

Here are some visual comparisons of the algorithm’s performance with and without key modifications:

Backtracking:

• Without backtracking, ants often got stuck in loops.
• With backtracking, the paths became more efficient and direct.

Visited Dictionary:

• Without the visited dictionary, ants frequently revisited nodes, leading to inefficiency.
• With the visited dictionary, redundant exploration was minimized.

Momentum:

• Without momentum, ants made unnecessary turns, resulting in longer paths.
• With momentum, the paths became smoother and more direct.

U-Turn Penalty:

• Without the U-turn penalty, ants often reversed direction, wasting time.
• With the U-turn penalty, movement became more purposeful and efficient.

Conclusion

By combining Genetic Algorithms and Ant Colony Optimization, I was able to create a robust solution to the Travelling Salesman Problem. The GA provided a broad exploration of the solution space, while the ACO refined the solutions to find the optimal route. The modifications I made to the ACO algorithm, such as backtracking, momentum, and U-turn penalties, significantly improved its efficiency and effectiveness.

This project was a great learning experience, and I’m excited to explore further optimizations and applications of these algorithms in the future. If you have any questions or suggestions, feel free to reach out!

The final solutions looked like this: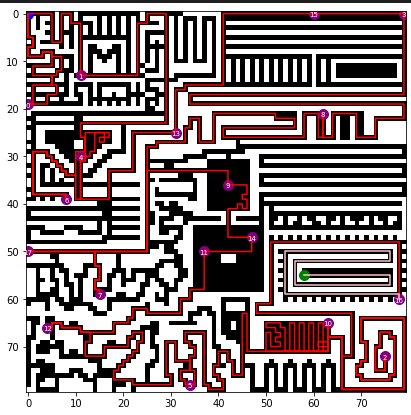

While Running the genetic algorithm for 500 gneration we converged to our most optimum route, as shown in the following graph.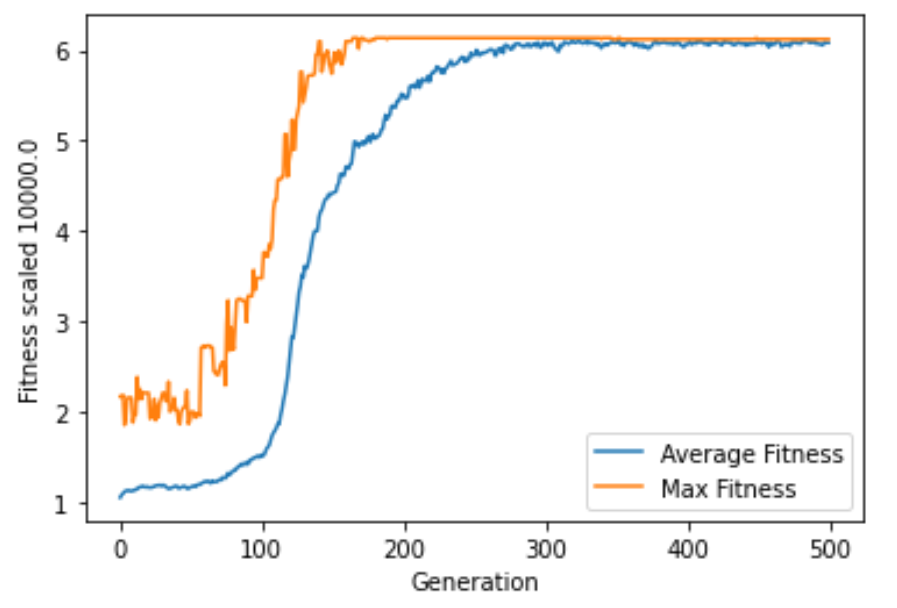

We had a final score of ~1600 route distance, but which was around the optimal solution for ~1300

Code and visualizations are available on GitHub.